Question

Given that k(x) = (2x + 4)2

Express k(x) in the form fq(x)where f(x) and g (x) are two simpler functions of x.

Answer 1

`f(x)=4x\\g(x)=x+2`

Explanation:

Because we have to rewrite this equation in the format
`f(g(x))`, we have to divide, or factor to find basic terms,

Expanding the value of k(x), we have
`k(x)=4x+8`. We see that each term can be divisible by 4, so we can factor out 4 to get

`k(x)=4(x+2)`

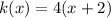
Now, we have two different terms getting multiplied. We can separate the two to get
`4 \text{ and} (x+2)`

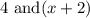
Because we are multiplying 4 by the other term, this is represented by
`4x`

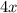
Now, we can just set f(x) and g(x) to these functions:

`f(x)=4x\\g(x)=x+2`

Now, just to make sure, we can plug a value into k(x) and the same value into f(g(x)). Plugging in 1, we have (2(1)+4)2 as 2(2+4), which is 2(6) = 12.

Plugging 1 into f(g(x)), we can evaluate g(1) first, to get 1 + 2 = 3. Now, f(3) = 4(3)= 12, which is the same for k(x).