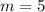Answer:
General Formulas and Concepts:
Pre-Algebra
Evaluations
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Algebra I
Coordinate Planes
Slope Formula:

Explanation:
Step 1: Define
Identify variables.
Point (4, 2)
Point (6, 7)
Step 2: Find slope m
Simply plug in the 2 coordinates into the slope formula to find slope m.
- Substitute in points [Slope Formula]:

- [Evaluations] Simplify:
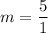
- [Evaluations] Simplify: