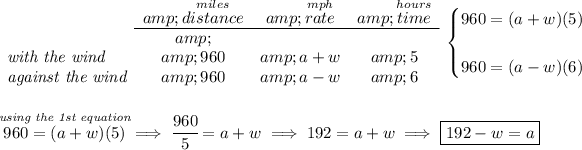Question

An airplane flying with the wind takes 5 hours to travel a distance of 960 miles. The return trip takes 6 hours flying against the wind. What is the speed of the airplane in still air and how fast is the wind blowing? ​

Answer 1

let's recall that d = rt, distance = rate * time.

a = speed of the airplane in still air.

w = speed of the wind

the distance travelled with the wind is 960 miles, so the return trip is pretty much just that, 960 miles.

when the airplane is going with with wind, the airplane is really not going as fast as "a" mph, is really going faster due to the wind, so the speed of the plane is "a + w", because the wind is adding its speed to it.

when the airplane is going against the wind is not really going "a" mph fast either, is really going slower at "a - w" mph, because the wind is subtracting speed from it, so

`\begin{array}{lcccl} &\stackrel{miles}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ \cline{2-4}&\\ \textit{with the wind}&960&a+w&5\\ \textit{against the wind}&960&a-w&6 \end{array}~\hfill \begin{cases} 960=(a+w)(5)\\\\ 960=(a-w)(6) \end{cases} \\\\\\ \stackrel{\textit{using the 1st equation}}{960=(a+w)(5)}\implies \cfrac{960}{5}= a + w\implies 192=a+w\implies \boxed{192-w=a}`

`\stackrel{\textit{substituting on the 2nd equation}}{960=(\underline{192-w}~~ - ~~w)(6)}\implies \cfrac{960}{6}=192-w-w\implies 160=192-2w \\\\\\ 2w+160=192\implies 2w=32\implies w=\cfrac{32}{2}\implies \blacktriangleright w=16 \blacktriangleleft ~\hfill \blacktriangleright \stackrel{192 - 16}{176=a} \blacktriangleleft`