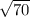Question

Can anyone help me please

Answer 1

NM =
`√(70)`

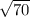
Explanation:

Δ NMO and Δ KML are similar ( by the AA postulate )

Then the ratios of corresponding sides are in proportion, that is

`(NM)/(KM)` =
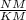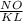`(NO)/(KL)` ( substitute values, noting KL = 2NM )

`(KM)/(29)` =
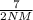`(7)/(2NM)` ( cross- multiply )

2 NM² = 140 ( divide both sides by 2 )

NM² = 70 ( take the square root of both sides )

NM =
`√(70)`

Answer 2

NM =
`\sf √(70)`

Explanation:

Let NM = y

If KL is twice the length of NM, then KL = 2y

Given:

• KM = 20
• NO = 7

As ΔKLN ~ ΔNOM

KL : KM = NO : NM

`\sf \implies 2y : 20 = 7 : y`

`\sf \implies (2y)/(20)=(7)/(y)`

`\sf \implies 2y \cdot y=7 \cdot 20`

`\sf \implies 2y^2=140`

`\sf \implies y^2=70`

`\sf \implies y=√(70)`

As NM = y, then NM =
`\sf √(70)`