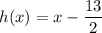Answer:
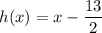
Explanation:
We are given that:

And we want to write the equation for the tangent to the graph of g at x = 4.
First, determine g(4):
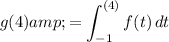
This is equivalent to the area of f from -1 to 4:
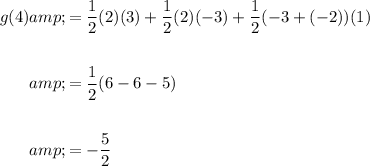
Note that areas under the x-axis are negative.
Find g'(4):
![\displaystyle \begin{aligned} g'(x) = (d)/(dx)\left[ \int_(-1)^x f(t)\, dt\right]\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/college/ed81o6gkkpspxxlxl5m30ddep3w4zo3ims.png)
By the Fundamental Theorem of Calculus:
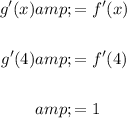
Note f is a line for 3 < x < 6 with a slope of 1.
Therefore:
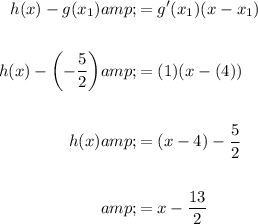
In conclusion, the equation of the tangent line is: