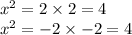1 Answer

Samjudson · Answer 1 · 2022-12-24T05:23:39+0000

Answer:

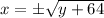
$x=\pm√(y+64)$

Explanation:

All you need to do is isolate the x.

First, add 64 to both sides:

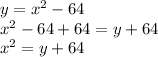
$y=x^2-64\\x^2-64+64=y+64\\x^2=y+64$

Then, take the square root of both sides:

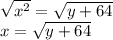
$√(x^2)=√(y+64)\\x=\sqrt{y+64$

Actually, that is:

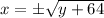
$x=\pm√(y+64)$

Here's the reason for that. An example would be:

x^2=4

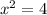
Here, you'd take the square root of both sides to solve for x.

$√(x^2)=√(4)\\x=2$

Right? But X could also be a -2, because a negative times a negative is a positive.

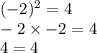
$(-2)^2=4\\-2*-2=4\\4=4$

Therefore,
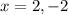x=2, -2 or
$x=\pm2$

$x^2=2*2=4\\x^2=-2*-2=4$

Please log in or register to add a comment.