To solve this problem, we can use conditional probability.
Let's assume that there were 100 students in the final exam.
According to the problem, 40% of the students failed chemistry, which means that 60% of the students passed chemistry.
- We can see that 25% of the students failed physics, and 19% of the students failed both chemistry and physics.
To find the probability that a randomly selected student failed physics given that he passed chemistry, we need to use Bayes' theorem:
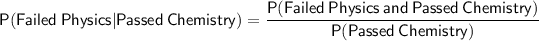
We already know that P(Failed Physics and Passed Chemistry) = 6 students (from the Venn diagram), and P(Passed Chemistry) = 60 students (since 60% of the students passed chemistry).
Therefore,

So the probability that a randomly selected student failed physics given that he passed chemistry is 10%.