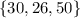Question

Identify next three numbers in this sequence: 2, 8, 4, 16, 12

Answer 1

2, 8, 4, 16, 12, 30, 26, 50

Explanation:

The first is determinate the different (
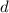`d`) between each consecutive value (
`a_n - a_(n-1)`).

`8 - 2 = 6\\4 - 8 = -4\\16 - 4 = 12\\12 - 16 = -4\\`

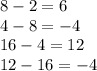
How you can see when the position of the number in the sequence is odd you have to sum a number
`6x` and when the position of the number in the sequence is a even number you have to substract -4.

Why
`6x`? If you see the first two odd position numbers in the sequence are multiples of 6, then we made the deduction that each time that you sum a number this is a multiply of 6 and -4 is constant for each position even number.

Then for each odd position number in the sequence it's representation is of the form:

`a_(n-1) + 6x = a_n`

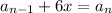
Where
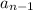`a_(n-1)` is the number of before,
`x` the odd position of the number in the sequence and
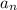`a_n` is the current value of
`a_n`

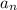
So the rest of the sequence is of the next form:

`12 + 6(3) = 30`

`30 -4 = 26`

`26 + 6(4) = 50`

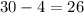
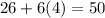
So the final answer is
`\{30, 26, 50\}`

Answer 2

The next three numbers are 48, 44, 176