Hello there,
- I just looked into the question and you are absolutely right whatever you inferred.
- I think the question might be wrong.
- The value of c should be greater than b.
- I guess it will like this:
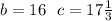
- The values should be like this.
- I am solving the equation by this:
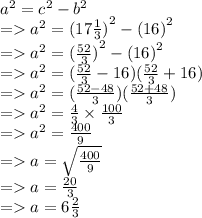
- So, the value of a is
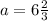
Hope you could get an idea from it.
Doubt clarification - use comment section.