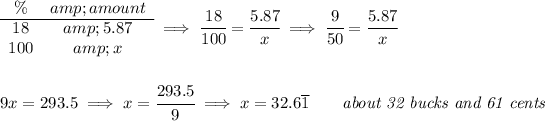Question

I need answers to all of these and explanation as well. Thank you.

Answer 1

4) d

let's firstly convert the mixed fractions to improper fractions, and then proceed

`\stackrel{mixed}{4(3)/(8)}\implies \cfrac{4\cdot 8+3}{8}\implies \stackrel{improper}{\cfrac{35}{8}}~\hfill \stackrel{mixed}{1(1)/(4)}\implies \cfrac{1\cdot 4+1}{4}\implies \stackrel{improper}{\cfrac{5}{4}} \\\\[-0.35em] ~\dotfill\\\\ -4(3)/(8)-\left( -1(1)/(4) \right)\implies -\cfrac{35}{8}-\left( -\cfrac{5}{4} \right)\implies -\cfrac{35}{8}+\cfrac{5}{4}\implies \cfrac{-(1)(35)~~ +~~(2)(5)}{\underset{\textit{using this as LCD}}{8}}`

`\cfrac{-35+10}{8}\implies -\cfrac{25}{8}\implies -3(1)/(8)`

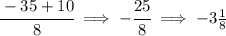
5)

hmmm we can pick any of those %, hmmm let's use 18%, keeping in mind that the whole amount is really the 100% and that's say "x", hmmm we know the 18% of "x" is $5.87.

`\begin{array}{ccll} \%&amount\\ \cline{1-2} 18&5.87\\ 100&x \end{array}\implies \cfrac{18}{100}=\cfrac{5.87}{x}\implies \cfrac{9}{50}=\cfrac{5.87}{x} \\\\\\ 9x = 293.5\implies x = \cfrac{293.5}{9}\implies x = 32.6\overline{1}\qquad \textit{about 32 bucks and 61 cents}`