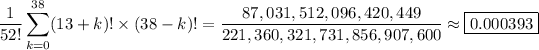In a given permutation of 52 cards, if the 3 of spades is to follow all of the hearts, that means the 3 of spades must be at least the 14th card in the deck.
Consider some possible orderings of the deck:
• If the 3 of spades is the 14th card, then the deck looks like
[all 13 ♥] … 3 ♠ … [all other 38 cards]
There are 13! ways to arrange the 13 hearts at the beginning and 38! ways to arrange the tail of 38 cards. Hence there are 13! × 38! possible rearrangements of the deck where 3 ♠ is the 14th card.
• If 3 ♠ is the 15th card, then the deck looks like
[13 ♥ and 1 other] … 3 ♠ … [all other 37 cards]
and there would be 14! × 37! ways of arranging the cards in this order.
There are 39 possible positions for 3 ♠. Extrapolating, it follows that the total number of permutations of the deck in which all hearts occur before 3 ♠ is
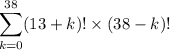
There are 52! total possible ways of rearranging the deck. Then the probability of rearranging the deck so that all hearts are drawn before 3 ♠ is