I assume you mean an angle of θ, and not 0. I also assume the given components of the initial velocity are horizontal and vertical, respectively, so that
1. the initial velocity vector is
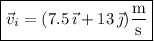
which means the ball is thrown with an initial speed of
√((7.5 m/s)² + (13 m/s)²) ≈ 15 m/s,
and
2. the angle made by
 with the positive horizontal axis is θ such that
with the positive horizontal axis is θ such that
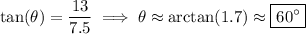
3. At time t, the ball attains a height y and horizontal range x according to
y = (13 m/s) t - g/2 t²
x = (7.5 m/s) t
where g = 9.8 m/s². When the ball reaches the ground (y = 0) for t > 0, we have
(13 m/s) t - g/2 t² = 0
13 m/s - g/2 t = 0
t = 2 (13 m/s)/g = (26 m/s)/g
Plugging this time into the x equation gives a horizontal range of
x = (7.5 m/s) (26 m/s)/g ≈ 20. m