Question

The zeros of a polynomial are 3/2 and 2/5. Find the polynomial.

___x²− ___x+6

Answer 1

Let the zeros of a polynomial be α and β.

Here,

• α:- 3/2
• β:- 2/5

Therefore to find the equation of polynomial we have to do sum of zeros of the polynomial and the product of zeros of the polynomial.

Sum of the zeros of polynomial are :-

`\sf \alpha + \beta = (3)/(2) + (2)/(5) \\ \\ : \rightarrow \: (15 + 4)/(10) = (19)/(10)`

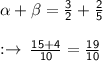
Product of the zeros of polynomial are:-

`\sf \: \alpha \beta = (3)/(2) * (2)/(5) \\ \\ : \rightarrow \cancel(6)/(10) = (3)/(5)`

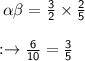
We know,

p(x) = x² - (α +β)x + αβ

putting values we get

p(x) = x² - 19/10x + 3/5

Hence, This is the required polynomial.