Question

Plz help me solve for x and y

Answer 1

x = 40°

y = 30°

Explanation:

Given parallelogram ABCD :

• ∠A = 3x°
• ∠B = 2y°
• ∠C = 120°
• ∠A = ∠C
• ∠B = ∠D
• ∠A + ∠B = 180°
• ∠B + ∠C = 180°
• ∠A + ∠B + ∠C + ∠D = 360°

∠A = ∠C

3x = 120

x = 120 ÷ 3

x = 40°

∠B + ∠C = 180°

2y + 120 = 180

2y = 180 - 120

2y = 60

y = 60 ÷ 2

y = 30°

Answer 2

x = 40°

y = 30°

Explanation:

Given the diagram of a parallelogram, where:

∠A = 3x°, ∠B = 2y°, and ∠C = 120°

The given problem also requires us to find the values of x and y.

In reference to the Parallelogram Opposite Angles Theorem, where it states that: if a quadrilateral is a parallelogram, then it will have congruent opposite angles. In other words, ∠A ≅ ∠C , and ∠B ≅ ∠D.

Solve for x:

Hence, we can establish the following equality statement to solve for the value of x:

m∠A = m∠C

3x° = 120°

Divide both sides by 3 to solve for x:

`\displaystyle\mathsf{(3x^(\circ))/(3)=\:(120^(\circ))/(3)}`

x = 40°

Therefore, the value of x = 40°.

Solve for y:

In order to solve for y, we must refer to the Parallelogram Consecutive Angles Theorem, where it states that if a quadrilateral is a parallelogram, then its consecutive angles are supplementary whose sum add up to 180°.

In the given diagram, ∠A and ∠D, ∠B and ∠C are consecutive angles.

We can establish the following equation to solve for the value of y:

m∠B + m∠C = 180°

2y° + 120° = 180°

Subtract 120° from both sides:

2y° + 120° - 120° = 180° - 120°

2y° = 60°

Divide both sides by 2 to solve for y:

`\displaystyle\mathsf{(2y^(\circ))/(2)=\:(60^(\circ))/(2)}`

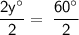
y = 30°

Therefore, the value of y = 30°.