Function: y = 5 sin (2(x))+ 12
Find y-intercept:
y = 5 sin 2(0)+ 12
y = 12
→ Formula for maximum: M = A + |B|
Maximum:
12 + |5|
17
When y = 17
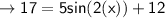
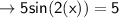
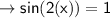
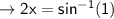
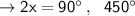
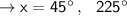
maximum: ( 45° , 17 ), (225° , 17), .....
==========================================================
→ Formula for minimum: m = A ‐ |B|
Minimum:
12 - |5|
7
When y = 7
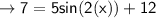
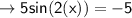
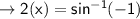
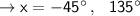
minimum: ( -45°,7), (135°, 7), .....
Repeat the same process for finding more values on the x-axis, or just follow the trend of the curve from the points found and sketch the graph easily.
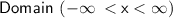
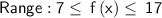
Sketched below: