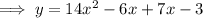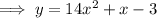Question

The zeros of a polynomial are −1/2 and 3/7. Find the polynomial.

___x²+x− ___

Answer 1

`y=14x^2+x-3`

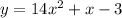
Explanation:

If the zeros of the polynomial are -1/2 and 3/7 then:

`\implies x=-\frac12`

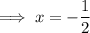
Add 1/2 to both sides:

`\implies x+\frac12=0`

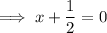
Multiply both sides by 2:

`\implies 2x+1=0`

`\implies x=\frac37`

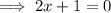
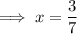
Subtract 3/7 from both sides:

`\implies x-\frac37=0`

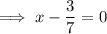
Multiply both sides by 7:

`\implies 7x-3=0`

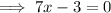
Therefore, the factored form of the polynomial is
`y=(2x+1)(7x-3)`

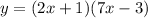
Expanding the brackets so that the polynomial is in standard form:

`\implies y=14x^2-6x+7x-3`

`\implies y=14x^2+x-3`