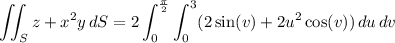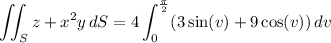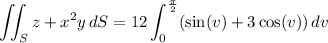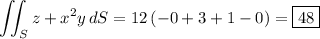Question

Evaluate the surface integral. S z + x2y ds s is the part of the cylinder y2 + z2 = 4 that lies between the planes x = 0 and x = 3 in the first octant.

Answer 1

Parameterize S in cylindrical coordinates by

s(u, v) = x(u, v) i + y(u, v) j + z(u, v) k

s(u, v) = u i + 2 cos(v) j + 2 sin(v) k

with 0 ≤ u ≤ 3 and 0 ≤ v ≤ π/2.

Take the normal vector to S to be

n = ∂s/∂v × ∂s/∂u

n = 2 cos(v) j + 2 sin(v) k

Then the norm of this vector is

||n|| = √((2 cos(v))² + (2 sin(v))²) = 2

so that the surface element is

dS = ||n|| du dv = 2 du dv

The surface integral is then

`\displaystyle \iint_S z + x^2y \, dS = 2 \int_0^(\frac\pi2) \int_0^3 (2\sin(v) + 2u^2 \cos(v)) \, du \, dv`

`\displaystyle \iint_S z + x^2y \, dS = 4 \int_0^(\frac\pi2) (3 \sin(v) + 9 \cos(v)) \, dv`

`\displaystyle \iint_S z + x^2y \, dS = 12 \int_0^(\frac\pi2) (\sin(v) + 3 \cos(v)) \, dv`

`\displaystyle \iint_S z + x^2y \, dS = 12 \left(\left( -\cos\left(\frac\pi2\right) + 3 \sin\left(\frac\pi2\right)\right) - \left( -\cos(0) + 3 \sin(0)\right)\right)`

`\displaystyle \iint_S z + x^2y \, dS = 12 \left(-0 + 3 + 1 - 0\right) = \boxed{48}`