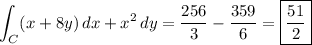Parameterize the path from (0, 0) to (8, 1) by
• x(t) = 8t and y(t) = t
and the path from (8, 1) to (9, 0) by
• x(t) = 8 + t and y(t) = 1 - t
both with 0 ≤ t ≤ 1.
Over the first path, we have
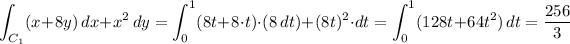
and over the second path,
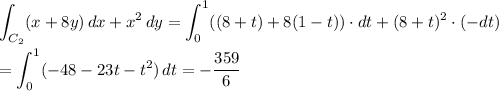
and so the total line integral is