Using the quadratic formula,
∆=b²-4ac
∆=(3√3)²-4(1)(6)
∆=(9×3)-4(6)
∆=27-24
∆=3
![x1 = ( - b - √(3) )/(2a) = ( - 3 √(3) - √(3) )/(2) = \frac{ - 4 \sqrt[]{3} }{2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/3913rvdom4z6g7rmmxnqea5oj3slqofdcj.png)
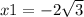
Similarly,
![x 2 = ( - b + √(3) )/(2a) = \frac{ - 3 √(3) + \sqrt[]{3} }{2} = ( - 2 √(3) )/(2)](https://img.qammunity.org/2023/formulas/mathematics/high-school/i00kccditl3t3k5mo7ei9ejo0i111uta7e.png)
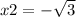
Method 2:
x²-Sx+P=0
where S is the sum of the roots & P is the product of the roots.
x¹+x²= -3√3
x¹x²=6
Solving the system you get the same answers.
Your factored equation can be written in the form of:
(x-x¹)(x-x²)
(x+2√3)(x+√3)