Question

What is the lim of (8n)/((3n^2)+5)?

Answer 1

We want to evaluate the limit of
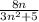`(8n)/(3n^(2)+5)` as n tends toward infinity (+∞)

The limit of this expression is the same as the limit of
`(8n)/(3n^(2))`

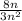
But this last expression can be simplified, we can remove one n up and down which gives us :
`(8)/(3n)`

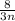
We know the limit of this one, it is simply Zero 0, by definition of the class lesson.

So to conclude the limit of
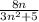`(8n)/(3n^(2)+5)` as n tends toward infinity is 0.

Good Luck

Answer 2

`\lim \limits_(n \to \infty) ~(8n)/(3n^2 +5) \\\\\\=8\lim \limits_(n \to \infty) ~ \frac{\tfrac n{n^2}}{\tfrac{3n^2}{n^2} + \tfrac 5{n^2}}\\\\\\=8 \lim \limits_(n \to \infty) ~\frac{ \tfrac 1n}{ 3 + \tfrac 5{n^2}}}\\\\\\=8 \cdot ( 0)/(3 +0) = 8 \cdot 0 = 0`