Answer:
3) f'(x) = x + 10
4) f'(x) = 6x - 18
5)
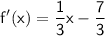 or
or
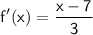
6) f'(x) = ⅛x or
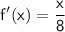
Explanation:
3. f(x) = x - 10
Step 1: In order to find the inverse function of f(x) = x - 10, start by replacing f(x) with y.
y = x - 10
Step 2: Switch x and y:
x = y - 10
Step 3: Add 10 to both sides to isolate y:
x + 10 = y - 10 + 10
x + 10 = y
Step 4: Replace y with f'(x):
f'(x) = x + 10 ⇒ This is the inverse function of f(x).
4.
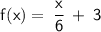
Replace f(x) with y:
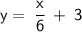
Switch x and y:
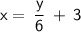
Subtract 3 from both sides:

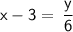
Multiply both sides by 6 to isolate y:
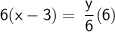
6x - 18 = y
Replace y with f'(x):
f'(x) = 6x - 18 ⇒ This is the inverse function of f(x).
5. f(x) = 3x + 7
Replace f(x) with y:
y = 3x + 7
Switch x and y:
x = 3y + 7
Subtract 7 from both sides:
x - 7 = 3y + 7 - 7
x - 7 = 3y
Multiply both sides by ⅓:
⅓(x - 7) = 3y (⅓)
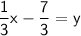
Replace y with f'(x):
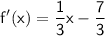 or
or
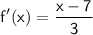 ⇒ This is the inverse function of f(x).
⇒ This is the inverse function of f(x).
6. f(x) = 8x
Replace f(x) with y:
y = 8x
Switch x and y:
x = 8y
Multiply both sides by ⅛:
⅛(x) = ⅛(8y)
⅛x = y or
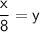
Replace y with f'(x):
f'(x) = ⅛x or
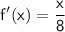 ⇒ This is the inverse function of f(x).
⇒ This is the inverse function of f(x).