Answer:
Option D: x = 5 ± 10i
Explanation:
Given the quadratic equation, y = x² - 10x + 125,
where:
a = 1, b = -10, and c = 125:
Use the following quadratic formula to solve for the roots:
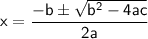
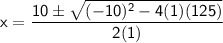
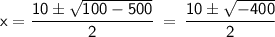
Apply the imaginary unit rule, where it states that:
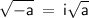 :
:
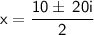
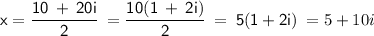
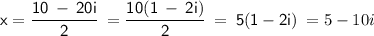
Therefore, the correct answer is Option D: x = 5 ± 10i .