Answer:
Solution 1:
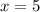
Solution 2:
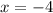
Explanation:
The first is organize the given equation to the next form

So you substract -20 in both sides of the equation
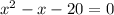
Know you can use the quadratic formula or find two number that sum give us
 and multiplied
and multiplied
 .
.
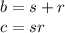
Replacing with the given values we have:

With a trial and error the numbers are -5 and 4. Then you change the equation to

And the equation is equal to 0 when
 is equal to 5 and -4.
is equal to 5 and -4.