Question

A triangle has angles with the following measures: (x2 + 34)°, (6x + 4)°, and (10x + 10)°. Solve for x. show all work please

Answer 1

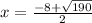`x = (-8 +√(190) )/(2)` or x = 5.7840

Explanation:

All the angles of a triangle add up to 180°, so we can solve this using the following equation:

180 = (x^2 + 34) + (6x + 4) + (10x + 10)

180 = x^2 + 34 + 6x + 4 + 10x + 10

Now, let's combine like terms:

180 = x^2 + (6x + 10x) + (34 + 4 + 10)

180 = x^2 + 16x + 54

Subtract 180 from both sides:

0 = x^2 + 16x - 126

And solve using the quadratic formula:

`x = \frac{-b +\sqrt{b^(2)-4ac } }{2a}\\x = \frac{-16 +\sqrt{16^(2)-4(1)(-126) } }{2(1)}\\x = (-16 +√(256+504 ) )/(2)\\x = (-16 +√(760) )/(2)\\x = (-16 +2√(190) )/(2)\\\\x = (-8 +√(190) )/(2)\\`

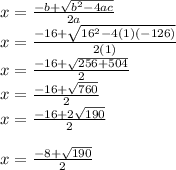
And we can approximate this as a decimal, if needed:

x = 5.7840