Answer:
y = -2/7(x) + 3
Explanation:
The equation of a line can be stated as y = mx + b, where m is the slope and b is the y-intercept (the value of the function when x = 0). To find the equation of the line, we'll start by finding the slope.
The slope can be expressed as
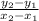
Substituting in our coordinates, we have:
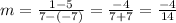 , which can be simplified to
, which can be simplified to
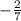
Plugging that back into our equation, we have y =
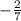 x + b
x + b
Now, to find b, we substitute in one of our sets of coordinates. Let's use (-7, 5)
x = -7 and y = 5, which gives us:
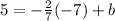
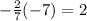 , which gives us:
, which gives us:
5 = 2 + b
Subtracting 2 from both sides, we get:
3 = b
Plugging that back into our equation, we have
