Question

Hii friends help me to do my homework

the zeroes of 3x² - 2x + 1/3 are real and equal justify ​

Answer 1

Explanation:

Proof using Discrimant:

`3 { x}^(2) - 2x + (1)/(3) = 0`

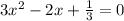
The discrimant is

`\sqrt{ {b}^(2) - 4ac}`

B is -2, A is 3 and C is 1/3 so we get

`\sqrt{ {2}^(2) - 4( 3)( (1)/(3)) }`

`√(4 - 4)`

`√(0 ) = 0`

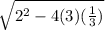
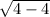
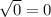
Since the discrimant equal zero, there is one real distinct zero.

This zero will also have a multiplicity of 2, so the zero is technically equal to each other.

To get better at solving, let solve for zero.

`3 {x}^(2) - 2x + (1)/(3) = 0`

`3( {x}^(2) - (2)/(3) x + (1)/(9) )`

`3( x - (1)/(3) )(x - (1)/(3) )`

`3(x - (1)/(3) ) {}^(2) = 0`

`x = (1)/(3)`

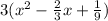
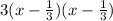
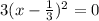
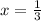
That zero is 1/3,1/3