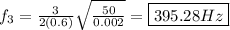Question

Find the first three harmonics of a string of linear mass density 2.00 g/m and length 0.600 m when it is subjected to tension of 50.0 N.

Answer 1

Hi there!

We can use the following equation to find the frequency of each harmonic:

`f_n = (n)/(2L) \sqrt{(T)/(\lambda)}`

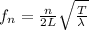
n = nth harmonic

L = length of string (m)

T = Tension of string (N)

λ = linear density (kg/m)

Begin by converting the linear mass density to kg:

2.00g /m · 1 kg / 1000g = 0.002 kg/m

Now, we can use the equation to find the first three harmonics.

First harmonic:

`f_1 = (1)/(2(0.6)) \sqrt{(50)/(0.002)} = \boxed{131.76 Hz}`

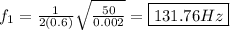
Second harmonic:

`f_2 = (2)/(2(0.6)) \sqrt{(50)/(0.002)} = \boxed{263.52Hz}`

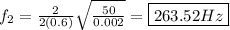
Third harmonic:

`f_3 = (3)/(2(0.6)) \sqrt{(50)/(0.002)} = \boxed{395.28Hz}`