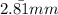Question

The area of a trapezoid is 65mm2, the top is

9mm long, the height is 11mm long.

Find the base of the trapezoid.

Answer 1

`2.\bar{81}mm`

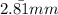
Explanation:

First the formula for find the are of a trapezoid is:

`A = (h(a+b))/(2)`

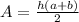
Where
`a` is the top,
`h` the height and
`b` the base measures.

Then we need to know what is the base (
`b`), for that isolate
`b` from the equation

`2A = h(a+b)\\(2A)/(h) = a+b\\(2A)/(h) - a = b`

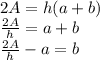
Then in the new equation replace the given values:

`A = 65mm^2\\a = 9mm\\h = 11mm`

`(2 \cdot 65mm^2)/(11mm) -9mm = b\\(130mm^2)/(11mm) -9mm = b\\11.\bar{81}mm -9mm = b\\2.\bar{81}mm = b`

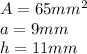
So the final answer is
`2.\bar{81}mm`