Answer:
a. The ball would reach the ground in approximately
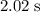 .
.
b. The velocity of the ball right before landing would be approximately
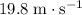 .
.
(Assumptions: the ball was dropped with no initial velocity; air resistance on the ball is negligible;
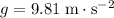 .)
.)
Step-by-step explanation:
Under these assumptions, the acceleration of this ball would be constantly
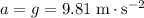 (same as the gravitational field strength) during the descent.
(same as the gravitational field strength) during the descent.
Displacement of the ball:
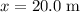 .
.
Initial velocity of the ball:
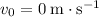 .
.
Let
 denote the duration of this descent.
denote the duration of this descent.
The SUVAT equation
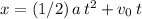 relates the known quantities
relates the known quantities
 ,
,
 , and
, and
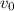 to the unknown
to the unknown
 .
.
Substitute the known quantities into this equation and solve to find the value of
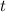 :
:
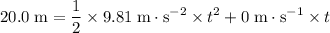 .
.
 .
.
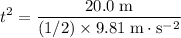 .
.
Since
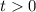 :
:
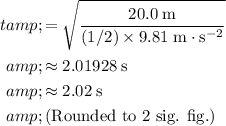 .
.
Since the acceleration of this ball is constant, the velocity of the ball right before landing would be:
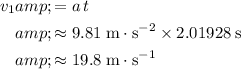 .
.