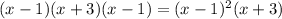Answer:
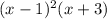
Explanation:
For factorization the given expression you can use the Ruffini's rule.
First find the divisors of the independent term (these are the possible rational roots), in the given polynomial the independent term is
 .
.
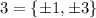
Now replace each number in the polynomial
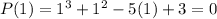
If the result is equal to 0 that's meaning that is a possible root of the polynomial. Then for know if is a root you have to divide the polynomial by
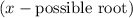 .
.
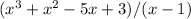
In the first row are the coefficients of the given polynomial.
In the second row are the product between the coefficients and the independent term of the
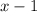 .
.
The third row are the coefficients of the quotient polynomial (except the last that is the remainder).
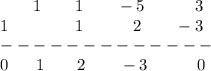
Because the last term is the remainder and it's 0 you can factorizate
 and the quotient polynomial is equal to
and the quotient polynomial is equal to
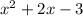
So our current expression is
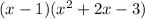 , however you can factorizate the quotient polynomial in:
, however you can factorizate the quotient polynomial in:
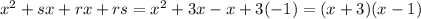
So the last expression is: