We are given that ;
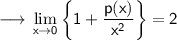
Where p(x) is a polynomial of degree 4 , it will help us later, but let's do some manipulations first ;
Can be further written as ;
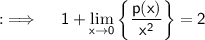
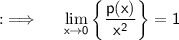
So, here p(x) is polynomial of degree 4, so it will be a biquadratic polynomial, so we will write p(x) in the form of general biquadratic polynomial, so p(x) = ax⁴ + bx³ + cx² + dx + e
Now, first find p(x)/x² ;
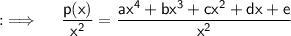
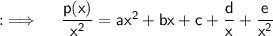
So now, as
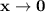 , for any values of a, b, c, d and e, the RHS will approach ∞ iff d ≠ e ≠ 0, as the denominator of d and e will be approaching 0 and so the whole limit will be ∞ , but we want the limit to be approaching 1, so when if d = e = 0, the denominator of d and e will be approaching 0 (not absolutely 0), and if d = e = 0, we will have the limit be approaching ax²+ bx + c for x approaching 0 being the limit 1 , and for any values of a, b and c . So now we have ;
, for any values of a, b, c, d and e, the RHS will approach ∞ iff d ≠ e ≠ 0, as the denominator of d and e will be approaching 0 and so the whole limit will be ∞ , but we want the limit to be approaching 1, so when if d = e = 0, the denominator of d and e will be approaching 0 (not absolutely 0), and if d = e = 0, we will have the limit be approaching ax²+ bx + c for x approaching 0 being the limit 1 , and for any values of a, b and c . So now we have ;
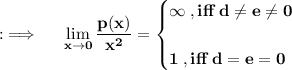
So, now we had to consider the second case, for which the limit is approaching 1, for d = e = 0, so the limand here will just be ax² + bx + c
Now, we so have ;
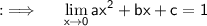
Putting the limit we will have ;

So, now as p(x) have extremum at 1 and 2, so p'(x) = 0, for x = 1, 2 , so now finding p'(x)
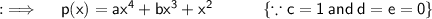
So, differentiating both sides wr.t.x ;
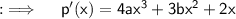
Now, p'(1) and p'(2) must be 0
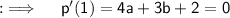
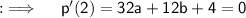
So, now we have ;
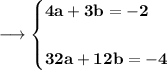
On multiplying first equation by 8 on both sides we can thus obtain ;
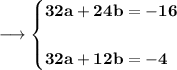
On solving both the equations we will be having ;
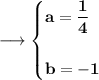
So , now as d = e = 0, c = 1, a = (1/4), b = -1, so putting all the values in p(x) we can obtain p(x) as ;
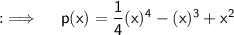
Now, at x = 2 ;
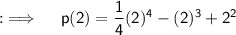
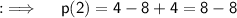
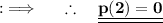
This is the required answer