Question

Find the slope of the line that goes through the points (4,-3) and (5,0)

Answer 1

the slope of the points (4,-3) and (5,0) is 3

Step-by-step explanation: I used the formula y2-y1 over x2-x1 will give you the answer hope this helped!

Answer 2

`\boxed {\boxed {\sf m=3}}`

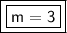
Explanation:

We are asked to find the slope of the line that passes through (4, -3) and (5,0).

The slope is the number that tells us the steepness and direction of a line. It is the rise over run, or the change in y over the change in x.

`m= ( \Delta y)/(\Delta x) = (y_2-y_1)/(x_2-x_1)`

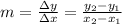
In the slope formula, (x₁, y₁) and (x₂, y₂) are the points the line passes through. The points we are given are (4, -3) and (5,0). If we match the value with its corresponding value, we see that:

• x₁ = 4
• y₁ = -3
• x₂ = 5
• y₂ = 0

Substitute the values into the formula.

`m= (0 - -3)/(5-4)`

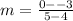
Solve the numerator. Remember that 2 back to back subtraction signs become an addition sign.

• 0--3 = 0+3=3

`m= (3)/(5-4)`

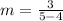
Solve the denominator.

• 5-4 =1

`m= (3)/(1)`

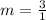
Divide.

`m=3`

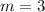
The slope of the line is 3.