Answer:

Explanation:
The average rate of change is the change in the output from one input to another. Essentially, it is the change in y over the change in x.
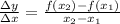
Let's assign 1 to x₁ and 5 to x₂.

We must find the outputs f(5) and f(1). Substitute the value in for each x in the function.
f(x)= 4x² + 3x
Now we can find the average rate of change. We know the outputs and we know the inputs.

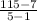
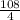

The average of change of the function f(x) = 4x² + 3x on the interval [1,5] is 27.