Question

Let f(x)=3-3x+5x^2.calculate the following.
f(a)=
f(a+h)=
f(a+h)-f(a)/h= for h≠0

Answer 1

Answer & step-by-step explanation:

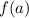`f(a)` is simply calculating by replacing a in lieu of x

`f(a) = 3-3a+5a^2`

Same difference for
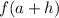`f(a+h)`, just be careful with products and squares:

`f(a+h) = 3-3(a+h)+5(a+h)^2 = 3-3a-3h+5a^2+10ah+5h^2 = 3-3a+5a^2 -3h+10ah+5h^2`

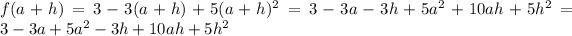
In the last step i just reorganized terms so that everything containing h was at the end.

Finally, for the incremental ratio, writing it as 1/h for the sake of font sizes:
`\frac{f(a+h)-f(a)}h = \frac1h[(3-3a+5a^2-3h+10ah+5h^2)-(3-3a+5a^2)]=\\\frac1h(-3h+10ah+5h^2) = 10a-3 +5h`