Question

PLEASE PLEASE HELP ME

Answer 1

Step-by-step explanation:

Note:

the text that is formatted in bold and underlined fonts are the answers to the missing (blank) terms in the given problem.

Answers:

Given that
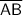`\huge\sf{\overline{AB}}` is a straight line, and that ∠AOE, ∠EOF, and ∠FOB share a common vertex, at point O, whose sum equals 180°.

1. Statement: m∠AOB = 180°

Reason: Definition of a straight angle.

2. Statement: m∠AOE + m∠EOF + m∠FOB = m∠AOB

Reason: Angle Addition Postulate.

3. Statement: x + (2x + 34) + 20° = 180°

Reason: Substitution.

4. Statement: x = 42°

Reason: Algebra.

Step-by-step explanation:

1) Straight angles have a measure of 180°.

2) The Angle Addition Postulate states that if O is in the interior of ∠AOB, then it means that the measure if ∠AOB is equal to the sum of the measures of ∠AOE, ∠EOF, and ∠FOB. In other words:

⇒
`\huge\bf\sf{m\angle{AOB}\:=m\angle{AOE}\:+m\angle{EOF}\:+m\angle{FOB}}`

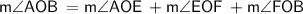
3) and 4) Since the ∠AOB is a straight angle, then it means that the sum of the measures of ∠AOE, ∠EOF, and ∠FOB equal the measure of ∠AOB = 180°. Hence, in order to solve for the value of x, simply add the given values for each angle:

x° + (2x + 34)° + 20° = 180°

x° + 2x° + 34° + 20° = 180°

Combine like terms:

3x° + 54° = 180°

Subtract 54° from both sides:

3x° + 54° - 54° = 180° - 54°

3x° = 126°

Divide both sides by 3 to solve for x:

`\huge\sf{(3x^\circ)/(3)\:=\:(126^\circ)/(3)}`

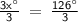
x = 42°