Answer: Choice C
==========================================================
Step-by-step explanation:
Recall that the form
![z = r*\left[\cos\left(\theta\right)+i*\sin\left(\theta\right)\right]](https://img.qammunity.org/2022/formulas/mathematics/high-school/xpea7ktpc24gwuhxmgciq46dlo6465jqha.png)
can be abbreviated to
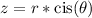
The "cis" stands for the first letters of "cosine i sine" in that order.
The original fairly messy quotient can be shortened down to

We have 90cis(pi/4) all over 2cis(pi/12) as one big fraction.
-------------------------------
Now we'll use this rule to divide two complex numbers

As you can see, we divide the r1 and r2 values to form the final coefficient out front. The theta angles are subtracted to form the new argument.
-------------------------------
Let's apply that idea to what your teacher gave you

That last step then converts directly to the expression shown in choice C.