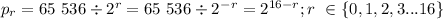Question

A huge Ping-Pong tournament is held in Beijing with 65,536 participants at the start of the tournament. Each round of

the tournament eliminates half the participants.
a.
If p(r) represents the number of participants remaining after r rounds of play, write a formula to model the
number of participants remaining.

Answer 1

`p_r = 65\ 536 / 2^r = 65\ 536 / 2^-^r = 2^(16-r); r\ \in \{0,1,2,3...16\}`

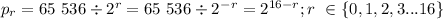
Explanation:

Pet peeve of mine: let's call it
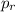`p_r` (read p sub r)since it's a representation over the natural numbers and not over
`\mathbb{R}`.

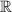Old man yelling at clouds moment gone, we know that the number of people gets halved every time so

At round 0, we do not halve, so
`p_0 = 65\ 536/ 1`

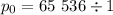
At round 1, we halve once, so
`p_1 = 65\ 536/ 2`

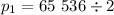
At round 2, we halve twice, so
`p_2 = 65\ 536/ 4 = 65\ 536/ 2^2`

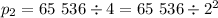
At round 3, we halve three times, so
`p_3 = 65\ 536/ 8 = 65\ 536/ 2^3`

...

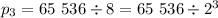
At round k, we halved k times, so
`p_k = 65\ 536 / 2^k`

...

At round 16 we
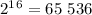`2^1^6 =65\ 536` so we have a winner.

That allows us to write a formula. I personally find the last one to be the neater, but any of the three is formally correct.

`p_r = 65\ 536 / 2^r = 65\ 536 / 2^-^r = 2^(16-r); r\ \in \{0,1,2,3...16\}`

Answer 2

`P(r)=65536((1)/(2))^(r)`

Explanation:

Since the total number of participants in the tournament is 65,536 people, and the exponential decay is
`(1)/(2)`, using
`P(r)` as the representative of the number of people after
`r` rounds, the formula to represent the model would be
`P(r)=65536((1)/(2))^(r)`.