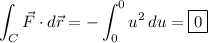Question

Use stokes' theorem to evaluate s curl f · ds. F(x, y, z) = x2 sin(z)i + y2j + xyk, s is the part of the paraboloid z = 1 − x2 − y2 that lies above the xy-plane, oriented upward.

Answer 1

The boundary of S is the unit circle C in the (x, y) plane with equation x² + y² = 1, which we can parameterize by

r(t) = x(t) i + y(t) j + z(t) k

with 0 ≤ t ≤ 2π, where

x(t) = cos(t)

y(t) = sin(t)

z(t) = 0

so that

dr = (dx/dt i + dy/dt j + dz/dt k) dt = (sin(t) i - cos(t) j) dt

By Stokes' theorem, the surface integral of the curl of F across S is equal to the line integral of F along C :

`\displaystyle \iint_S \mathrm{curl} F \cdot d\vec s = \int_C \vec F \cdot d\vec r`

We have

`\vec F(x(t), y(t), z(t)) = \sin^2(t) \, \vec\jmath + \sin(t) \cos(t) \, \vec k`

`\implies \vec F \cdot d\vec r = -\sin^2(t)\cos(t) \, dt`

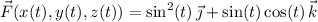
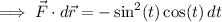
so the line integral is

`\displaystyle \int_C \vec F \cdot d\vec r = - \int_0^(2\pi) \sin^2(t) \cos(t) \, dt`

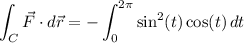
Substitute u = sin(t) and du = cos(t) dt :

`\displaystyle \int_C \vec F \cdot d\vec r = - \int_0^0 u^2 \, du = \boxed{0}`