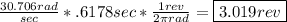Question

A solid sphere is released from the top of a ramp that is at a height

h1 = 2.20 m.
It rolls down the ramp without slipping. The bottom of the ramp is at a height of
h2 = 1.87 m
above the floor. The edge of the ramp is a short horizontal section from which the ball leaves to land on the floor. The diameter of the ball is 0.14 m.
a.) Through what horizontal distance d, in meters, does the ball travel before landing?
b.) How many revolutions does the ball make during its fall?

Answer 1

Hi there!

We can use the work-energy theorem and apply it to this situation.

At the top of the ramp, the ball only has gravitational potential energy, and at the bottom of the ramp, the ball has BOTH translational and rotational kinetic energy.

We must use the following equations:

`GPE = mgh \\KE_T = (1)/(2)mv^2\\\\KE_R = (1)/(2)I \omega^2`

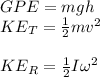
m = mass of sphere (kg)
g = acceleration due to gravity (m/s²)

h = height of ramp (m)

v = final velocity (m/s)
I = Moment of Inertia (kgm²)

ω = angular velocity (rad/sec)

Since:

`E_i = E_f\\\\mgh = (1)/(2)mv^2 + (1)/(2)I\omega ^2`

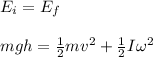
In order to make things easier, since the ball is not slipping, we can relate angular velocity to translational velocity:

`\omega = (v)/(r)`

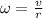
Also, recall the equation for the moment of inertia for a solid sphere:

`I = (2)/(5)mr^2`

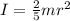
We can use these to simply our equation:

`KE_R = (1)/(2)((2)/(5)mr^2)((v)/(r))^2 = (1)/(5)mv^2`

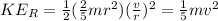
Now, we can rewrite the equation and solve for 'v'.

`mgh = (1)/(2)mv^2 + (1)/(5)mv^2\\\\mgh = (7)/(10)mv^2\\\\v = \sqrt{(10gh)/(7)} = \sqrt{(10(9.8)(2.2 - 1.87))/(7)} = 2.149(m)/(s)`

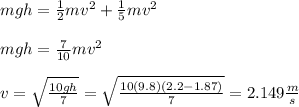
a)

We can begin by solving for the time taken for the ball to land on the ground. The ball only has a horizontal velocity, so this is essentially a free-fall situation. Use the rearranged kinematic equation:

`t = \sqrt{(2h)/(g)} = \sqrt{(2(1.87))/(9.8)} = .6178 s`

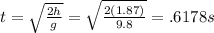
Now, use the following equation to solve for horizontal distance given horizontal velocity and time:

`d_x = v_x t\\\\d_x = 2.149 * .6178 = \boxed{1.328 m}`

b)
We can use the previously-stated relationship between translational and angular velocity to solve for the angular velocity.

`\omega = (v)/(r)`
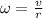
It is given that the diameter is 0.14 m, so the radius is 1/2th the diameter, or 0.07 m.

Solve for the angular velocity:

`\omega = (2.149)/(0.07) = 30.706 (rad)/(sec)}`

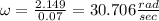
Using the above fall time and dimensional analysis to convert from rad/sec to revolutions, we can solve for the # of revolutions made by the ball:

`(30.706rad)/(sec) * .6178 sec * (1 rev)/(2\pi rad) = \boxed{3.019 rev}`