Since you have the answers, I'll just show the steps on how to get there.
============================================================
Problem 19
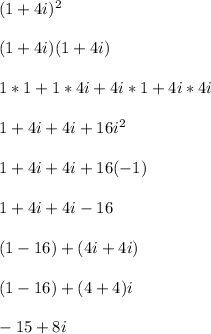
Keep in mind that
 by definition. Squaring both sides leads to
by definition. Squaring both sides leads to
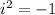
In the second step, I used the idea that x^2 = x*x. Right after that, I used the FOIL rule to expand everything out.
============================================================
Problem 21
We could follow the same idea as problem 19, but I'll use a different approach.
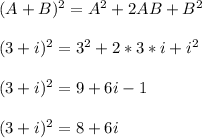
The formula on the first line is the perfect square binomial formula.
============================================================
Problem 23
The FOIL rule can be used if you want, but I'll use the difference of squares rule instead.
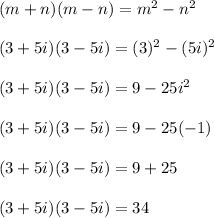
It turns out that multiplying any complex number of the form a+bi with its conjugate a-bi will result in a purely real number (that has no imaginary part). More specifically:
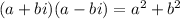
============================================================
Problem 25
We could use the difference of squares rule again, but I'll show a different approach. This time using the distribution rule. The FOIL rule could also be used if you wanted.

I used x = 6+7i and the substitution property to help distribute. Lines 3 and 6 are where distribution is applied.