Question

A delivery truck is transporting boxes of two sizes: large and small. The combined weight of a large box and a small box is 70 pounds. The truck is transporting

50 large boxes and 70 small boxes. If the truck is carrying a total of 4100 pounds in boxes, how much does each type of box weigh?

Answer 1

Answers:

one small box = 30 pounds

one large box = 40 pounds

==========================================================

Work Shown:

• S = weight of one small box
• L = weight of one large box

S+L = 70 since the two boxes combine to 70 pounds.

70S = weight of 70 small boxes

50L = weight of 50 large boxes

70S+50L = weight of 70 small and 50 large

70S+50L = 4100

The system of equations is

`\begin{cases}S+L = 70\\70S+50L = 4100\end{cases}`

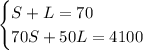
There are a few ways to solve this system. I'll use substitution.

I'm going to isolate L in the first equation like so

S+L = 70

L = 70-S

Which I'll then plug into the other equation to solve for S

70S+50L = 4100

70S+50(70-S) = 4100

70S+3500-50S = 4100

20S+3500 = 4100

20S = 4100-3500

20S = 600

S = 600/20

S = 30

Each small box is 30 pounds.

Use this value of S to find L

L = 70-S

L = 70-30

L = 40

Each large box is 40 pounds.

Like we expect, each large box weighs more compared to any given small box.

------------------

Check:

• S+L = 30+40 = 70 verifies the first equation
• 70S+50L = 70*30+50*40 = 4100 verifies the second equation

Both equations are true for the ordered pair (S,L) = (30,40). Therefore, the answers have been confirmed.