Answer:
55°
Explanation:
Let's start by finding "y" (see diagram attached).
Using the given diagram, we can conclude that the angle measuring 125° and angle y are a linear pair or supplementary. This means that they add up to 180°.
We can use this information to set up an equation:
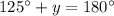
Subtract 125° from both sides:
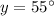
The diagram displays two parallel lines cut by a transversal.
Therefore "x" and "y" are corresponding angles.
The corresponding angle theorem states that if the two lines being cut by a transversal are parallel, then corresponding angles must be congruent/equivalent.
Using this theorem we can set up an equation...

Therefore...
