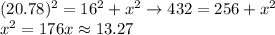Question

How many inches is the box's side?

And please explain how you found the answer
Thank you :)

Answer 1

`x\approx 13.27 in`

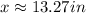
Explanation:

I'm assuming 24' is the diagonal of the box (red dashed line) and not of the bottom face (black dotted line).

Option 1: easiest if you know/remember the formula for the distance of two points in space (or for the diagonal of a parallelepiped):
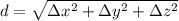`d= √(\Delta x^2+\Delta y^2+\Delta z^2)` where replacing (and squaring both sides to get rid of the square root) we get

`24^2 = x^2 + 16^2+12^2 \rightarrow 576= x^2+256+144 \rightarrow x^2=176\\x\approx13.27 in`

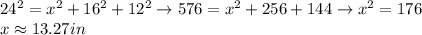
Option 2: look at the triangle that has sides the forward left edge of the box, the dotted diagonal and the dashed diagonal. It's a right triangle of hypotenuse 24 and side length 12. Pythagorean theorem to find the missing side lenght

`24^2 = l^2+12^2 \rightarrow l^2 = 432 \rightarrow l\approx 20.78 in`

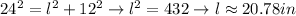
At this point we're back at the right triangle of the bottom face of the box, of hypotenuse 20.78' and side lenght 16'. Phythagorean theorem again:

`(20.78)^2= 16^2 +x^2 \rightarrow 432 = 256+x^2\\x^2 = 176 x \approx 13.27`