Answer:
The equation for the nth term of the arithmetic sequence is:
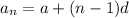
The
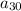 is 140
is 140
Explanation:
"a" represents the first term which is -5.
"d" represents the common difference which is 5.
To find the common difference, just subtract the 2nd and 1st term.
0 - (-5) = 5
Now put the values in the equation:
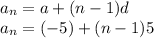
We are finding the 30th term so just put 30 to the "n" to help us find the 30th term of the sequence.
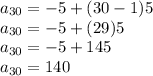
So the 30th term is 140