Question

Some spiders, dragonflies, and houseflies are kept in three separate enclosures. They have a total of 20 heads, 136 legs, and 19 pairs of wings.

Given that...
a spider has 8 legs and 0 pairs of wings
a dragonfly has 6 legs and 2 pairs of wings
a housefly has 6 legs and 1 pair of wings
Find the number of spiders, the number of dragonflies, and the number of houseflies.

Answer 1

Number of Spiders: 8

Number of Dragonflies: 7

Number of Houseflies: 5

Explanation:

s= spider

d= dragonfly

h= housefly

Heads:

20= s+d+h

Legs:

136= 8s+6d+6h

Wings:

19= 0s+2d+1h

Solve with substitution.

Divide the second equation by 2.

136= 8s+6d+6h

68= 3d+3h+4s

Set the last equation in terms of d.

19= 0s+2d+1h

d=
`(19)/(2) -(1)/(2)h`

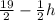
Substitute what we just found (d) into the first and our new second equation. Simplify.

20= s+d+h

20= s+
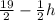`(19)/(2) -(1)/(2)h`+h

h+2s=21

68= 3d+3h+4s

68= 3(
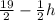`(19)/(2) -(1)/(2)h`)+3h+4s

3h+8s=79

Take both simplified equations and solve with elimination. Do this by multiplying the top equation by negative 3.

h+2s=21

3h+8s=79

-3h-6s=-63

3h+8s=79

2s=16

s=8

Plug in s=8 into the other equation.

h+2s=21

h+2(8)=21

h=5

Plug in h=5 into the last equation we rewritten.

`d= (19)/(2) -(1)/(2) h`

`d=(19)/(2) -(1)/(2)(5)`

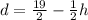
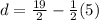
d=7

(d,h,s)= (7,5,8)