Question

I need answer please​

Answer 1

60°

Explanation:

Given:

QP and QR are tangent segments

∠PCR = 120°

Find:

∠PQR

Tangent lines always intersect a circle at one point. This means that the line from the center of the circle to the point of intersection would be the radius. This also means that the tangent line is perpendicular to the radius of the circle.

Therefore...

∠CPQ=90°

∠CRQ=90°

Using the diagram, we can conclude that Figure CPQR is a quadrilateral. We need to find the sum of the interior angles of the Figure CPQR.

The formula to find the sum of the interior angles of a figure is...

`(n-2)*180`

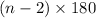
Note that n represents the amount of sides the figure has.

In this case Figure CPQR has 4 sides therefore...

`(4-2)*180=2*180=360^(\circ)`

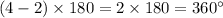
Now let's set up an equation to find ∠PQR...

∠PCR + ∠CPQ + ∠CRQ + ∠PQR = 360°

Substitute the measures of the known angles into the equation:

120° + 90° + 90° + ∠PQR = 360°

120° + 180° + ∠PQR = 360°

300° + ∠PQR = 360°

Subtract 300° from both sides

∠PQR = 60°