Question

What are the values of the two angles?

Answer 1

the angle 3x is 42 degrees, the angle 12x-30=138 degrees

Explanation:

first, write an equation to represent the problem.

3x+(12x-30)=180

3x+12x=210

15x=210

x=14

Answer 2

See below:

Explanation:

Hello! My name is Galaxy and I will be helping you today. I hope you are having a nice day.

We can solve this problem in 2 steps, one being Theory and the second being Solving. I'll start off with Theory.

Theory

There are many theorems in Geometry, from the very simple to the very complex, you also have got the standard information that is usually known by many people.

In this case, we can see that it is a Supplementary Angle. We know that Supplementary Angles add up to 180 degrees and Complementary Angles add up to 90 degrees.

Now that we know that we can solve the problem.

Solving

So, we know that both angles have to add up to 180 degrees because the line is a straight line and that means that the angles on it must be 180 degrees.

Since we know this, we can state the following equation:

`3x+12x-30=180`

We can say this due to the rule of Supplementary angles adding up to 180 degrees.

We can now use Algebra to simplify the equation:

`3x+12x-30=180\\3x+12x=210\\15x=210\\x=14`

After doing algebra we can see that x s equal to 14 degrees, we can check our answers by putting that back into the equation.

`3(14)+12(14)-30=180?\\42+168-30=180?\\210-30=180?\\180=180`

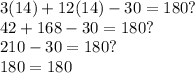
We have proven that our answer is correct, therefore the answer is
`x=14` degrees.

Cheers!