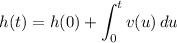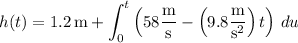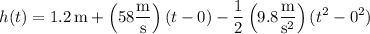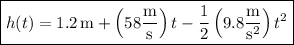If v(t) and h(t) denote the ball's velocity and height at time t, respectively, then we have h(0) = 1.2 m and v(0) = 58 m/s.
The ball is in free fall after being tossed, so its acceleration is constant at any time t :
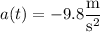
By the fundamental theorem of calculus, the velocity function is given by
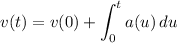
Compute the integral:
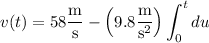
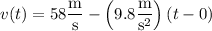
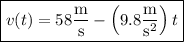
Similarly, the height function is given by