Given that :
- Thirteen is reduced by two-thirds of a number. And their result is 7.
To Find :
Solution :
Let's assume the number as x
According to the question :

Adding 13 to both sides we get :

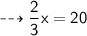
Now, Multiplying both sides by
 we get :
we get :
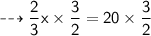
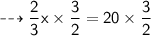

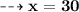
Therefore, The number is 30.