Question

Find the equation of the line that has a slope of 1 and passes through the point (−10,−6).

Answer 1

See below.

Explanation:

Hi there!

We want to find the equation of the line that has a slope (m) of 1 and that passes through the point (-10, -6)

There are 3 ways to write the equation of the line:

• Slope-intercept form, which is y=mx+b, where m is the slope and b is the y intercept
• Point-slope form, which is
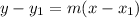  `y-y_1=m(x-x_1)`, where m is the slope and
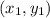  `(x_1, y_1)` is a point
• Standard form, which is ax+by=c, where a, b, and c are free integer coefficients, but a and b cannot be equal to zero, and a cannot be negative

Since we are given both a point and a slope in this situation, it makes sense to write the equation in point-slope form.

Let's label the values of everything we were given to avoid confusion and mistakes:

m=1

`x_1=-10\\y_1=-6`

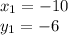
Now substitute these values into the equation (note: we have NEGATIVE numbers, while the formula gives SUBTRACTION, which is why we're subtracting a negative)

`y-y_1=m(x-x_1)`

`y--6=1(x--10)`

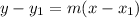
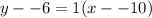
Simplify:

y+6=1(x+10)

The equation can be left as this, or it can be converted into slope-intercept form if you wish.

In that case, we would distribute 1 to each number on the right side.

y+6=x+10

Then, we'll isolate y on one side. Subtract 6 from both sides.

y=x+4

You can also convert it into standard form if you would prefer it that way. To do that, start with slope-intercept form, which we earlier found as y=x+4

In standard form, x and y are on the same side. So subtract x from both sides to move it

-x+y=4

Remember we don't want a (the coefficient in front of x) to be negative. In order to flip the sign, multiply both sides by -1

x-y=-4

Therefore, the answer can be written as y+6=1(x+10), y=x+4, or x-y=4.

Hope this helps!